Square Root 1 to 30

In the study of Mathematics, the square root of a number is defined as a number that if multiplied by itself then results in the original number. The square root of any number can be both negative and positive values. It is denoted by the radical symbol (√) and is used to find the side length of a square with a given area or to solve quadratic equations. The square root of any number (x) in radical form is expressed as √x and in the exponential form it is expressed as (x)½ For example, the square root of 16 is 4. If 4 is multiplied by 4, then we have 9.

The positive values of square roots of numbers from 1 to 30 cover the range from 1 to 5.477. In this article, you will get to know more about the values of square roots 1 to 30, the list and chart of square roots of numbers from 1 to 30, methods to find out the square roots, and solved examples.

What is the Square Root 1 to 30?

The square root of a number from 1 to 30 is generally expressed as √x. But in the case of the exponential form, the square root is expressed by x^(½), where x = 1 to 30 numbers. For example, √49 = 7.

Here, x = 49

Hence, the value of the square root of 49 is 7.

Square Root 1 to 30 Chart

The square root 1 to 30 chart helps you to quickly learn the values of the square roots of numbers from 1 to 30. It also simplifies the time-consuming long equations. The value of square roots of numbers from 1 to 30 up to 3 decimal places is listed below.

Square Root from 1 to 30 Chart
√1 = 1	√2 = 1.414
√3 = 1.732	√4 = 2
√5 = 2.236	√6 = 2.449
√7 = 2.646	√8 = 2.828
√9 = 3	√10 = 3.162
√11 = 3.317	√12 = 3.464
√13 = 3.606	√14 = 3.742
√15 = 3.873	√16 = 4
√17 = 4.123	√18 = 4.243
√19 = 4.359	√20 = 4.472
√21 = 4.583	√22 = 4.690
√23 = 4.796	√24 = 4.899
√25 = 5	√26 = 5.099
√27 = 5.196	√28 = 5.292
√29 = 5.385	√30 = 5.477

For faster maths calculations, students are suggested to memorize the square roots 1 to 30 values thoroughly.

Square Root 1 to 30 for Perfect Square Number

In square roots 1 to 30, the numbers 1, 4, 9, 16, and 25 are considered the perfect squares, and the remaining numbers are called the non-perfect squares. The square root of 1 is the only whole number whose square root is equal to itself. The following given table describes the values of square roots from 1 to 30 for perfect square numbers.

Square Root 1 to 30 for Perfect Square Number

√1 = 1
√4 = 2
√9 = 3
√16 = 4
√25 = 5

Square Root 1 to 30 for Non-Perfect Square Number

Excluding the numbers 1, 4, 9, 16, and 25, all numbers from 1 to 30 are considered non-perfect square numbers (their square root will be in irrational form). The following given table describes the values of square roots from 1 to 30 for non-perfect square numbers.

Square Root 1 to 30 for Non-Perfect Square Number
√2 = 1.414	√3 = 1.732
√5 = 2.236	√6 = 2.449
√7 = 2.646	√8 = 2.828
√10 = 3.162	√11 = 3.317
√12 = 3.464	√13 = 3.606
√14 = 3.742	√15 = 3.873
√17 = 4.123	√18 = 4.243
√19 = 4.359	√20 = 4.472
√21 = 4.583	√22 = 4.690
√23 = 4.796	√24 = 4.899
√26 = 5.099	√27 = 5.196
√28 = 5.292	√29 = 5.385
√30 = 5.477

How to Calculate Square Root 1 to 30?

Mainly there are two methods given below for calculating the values of square roots of numbers from 1 to 30.

Method 1- Prime Factorization

For perfect square numbers like 1, 4, 9, 16, and 25, the prime factorization method can be used to find square roots easily.

Question: Find out the value of √81 by using the prime factorization method.

Solution: The prime factorization of 81 is 9 × 9

Here, the pairing prime factors are 9

Thus, the value of √81 is 9.

Method 2- Long Division Method

For non-perfect square numbers like 2, 3, 5, 6, 7, 8, 10, etc., the long division method can be used.

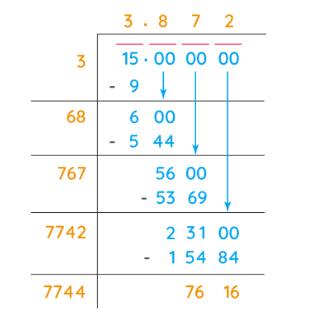
Question: Find out the value of √15 by using the long division method.

Solution:

Square Root 1 to 30 Solved Questions

Question 1: Find out the value of the square root of 324.

Solution: By using the prime factorization method,

We get, 324 = 2 x 2 x 3 x 3 x 3 x 3

√324 = √(2 x 2 x 3 x 3 x 3 x 3)

√324 = 2 x 3 x 3 = 18

Question 2: Solve out for the square root of 8.

Solution: By using the prime factorization method,

We get, 8 = 2 x 2 x 2

√8 = √(2 x 2 x 2) = 2√2

Question 3: A square plastic board has an area of 64 sq. inches. Solve out the length of the side of that plastic board.

Solution: Suppose x is the length of the side of the plastic board

Area of the square plastic board = 64 inches²= a²

a² = 64

a = √64 = 8 inches

Hence the length of the side of the plastic board is 8 inches.

Question 4: When a circular carpet has an area of 36π sq. inches. Calculate the radius of that carpet.

Solution: Given that the area of circular carpet = 36π in² = πr²

After canceling π on both sides, we get 36 = r²

Hence, radius = √36 = 6 inches

Question 5: Calculate the value of 3√7 + 2√10

Solution: Putting the value of √7 = 2.646 and √10 = 3.162, we get

3√7 + 2√10 = 3 × (2.646) + 2 × (3.162)

Hence, 3√7 + 2√10 = 7.938 + 6.324 = 14.262

Square Root 1 to 30: FAQs

The square root of a number is defined as a number that if multiplied by itself then results in the original number.

The square root of a number from 1 to 30 is generally expressed as √x. Within the range of 1 to 30, the square roots of numbers 1, 4, 9, 16, and 25 are whole numbers that are in rational form. The square roots of numbers 2, 3, 5, 6, 7, 8, 10, 11, 12, 13, 14, 15, 17, 18, 19, 20, 21, 22, 23, 24, 26, 27, 28, 29, 30 are decimal numbers that are in irrational form.

For perfect square numbers like 1, 4, 9, 16, and 25, the prime factorization method can be used and for non-perfect square numbers like 2, 3, 5, 6, 7, 8, 10, etc., the long division method can be used.

The numbers 1, 4, 9, 16, and 25 are perfect squares in square roots 1 to 30. Their square roots will be whole numbers that can be written in the form of p/q where q ≠ 0. Hence these numbers are rational.

The value of the square root of 30 is 5.477.

The square root of 1 is 1 (√1 = 1).